V kabinetech matematiky máme většinou pomůcky, které dodaly specializované firmy (Komenium atd.). Často však potřebujeme třeba ne tak technicky dokonalé, ale pro výuku velmi potřebné jednoduché pomůcky, které – podle zákona schválnosti – ve škole nejsou.
Není to žádná katastrofa, dokonce je někdy výhodné, že musíme improvizovat nebo si potřebnou pomůcku (nejlépe společně se žáky) vyrobit. Zkušenosti získané při tvorbě modelu nám totiž o modelovaném tělese prozradí mnohem více než pozorování hotových „exponátů“ naší sbírky. Slovní popis viděného se stává někdy jen formální záležitostí, ale zážitek činnosti, během níž se nám vlastní výrobek v rukou rodí, je velmi trvalý. Podílí se na něm rozumová úvaha, představivost, zrak i hmat. Slovní formulace korunující celé dílo je po takové zkušenosti určitě plná významů.
Během školní docházky se žáci v matematice seznamují s vybranými geometrickými tělesy (krychle, kvádr, rotační válec, kolmé hranoly atd.). Příčiny tohoto omezení jsou nasnadě. Domnívám se však, že bychom měli vzít na vědomí i důvody, z nichž vyplývá, že je třeba ukázat dětem i další tělesa, jejichž vlastnosti se od ostatních vybraných těles v něčem liší.
Teprve tehdy, až se naučíme bezpečně poznávat daná tělesa mezi jinými, jim podobnými, můžeme doufat, že je známe. Rovněž tak „podstata vzorců“, kterých užíváme, je nám jasná až ve chvíli, kdy nejen „správně dosadíme a vypočítáme“, co jsme vypočítat měli, ve standardní situaci, ale smysluplně je užijeme v situacích, které již nejsou tak běžné, a bezpečně rozeznáme, kdy jich užít nelze vůbec. Např. Vzorec pro výpočet obsahu obdélníku má mnoho dětí „v hlavě uložen“ takto: Obsah obdélníku vypočítám jako součin délek jeho stran – důležitějším znakem se stává ona „délka stran“ než pravý úhel, který sousední strany obdélníku svírají. Tato chyba je korigována až ve chvíli, kdy se začneme s dětmi zabývat kosočtverci a kosodélníky.
Obdobně zavádějící jsou představy o hranolech, jejich pláštích a objemech, jestliže vše demonstrujeme pouze na hranolech kolmých. Přitom by nám stačil jeden jednoduchý model, na němž bychom mohli demonstrovat, co je a co není podstatné pro výpočet objemu či tvorbu sítě kolmého hranolu. Jeden vhodný čtyřboký kosý hranol vám tento nápadník nabízí.
Matrice M: KOSÝ ČTYŘBOKÝ HRANOL
Vyjděme z kvádru, jehož strany mají délky 8 cm, 5 cm a 12,5 cm. Jeho objem je tedy 500 cm3. Pokud model tohoto kvádru šikmo seřízneme a obě takto získané části k sobě přilepíme původními podstavami, získáme model rovnoběžnostěnu, tj. Kosého čtyřbokého hranolu. Protože pomocí modelu budeme jistě chtít demonstrovat výpočet objemu (a případně i tvorbu sítě pomocí „kolmého řezu“), povedeme šikmý řez tak, aby rozměry podstavy (tj. čtyřúhelníku řezu původního kvádru) i výška hranolu byla „pěkná čísla“. Abychom dále mohli obou částí použít např. Také k modelování dvojic těles souměrných podle dané roviny atd., rozřízneme náš model kvádru na dvě shodné části
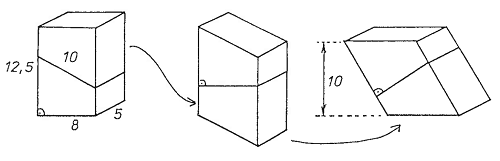
Na obrázku je znázorněn postup tvorby modelu z dřevěného kvádru. Příslušné rozměry jsou uvedeny v centimetrech. Výška získaného hranolu je 10 cm, rozměry jeho podstavy jsou 5 cm a 10 cm. Protože z obou částí lze sestavit kvádr i hranol, je zjevné, že obě tělesa mají stejný objem. Na šikmém hranolu snadno ověříme vzorec pro výpočet objemu hranolu, jehož výška je 10 cm. Obráceně můžeme za podstavu zvolit některou jinou jeho stěnu a příslušnou výšku vypočítat ze známého objemu a obsahu nové podstavy.
Model kosého hranolu
(zde jednoho krásného dne BUDE stáhnutelný PDF soubor s matricí v měřítku, zde zobrazený je pro ilustraci)
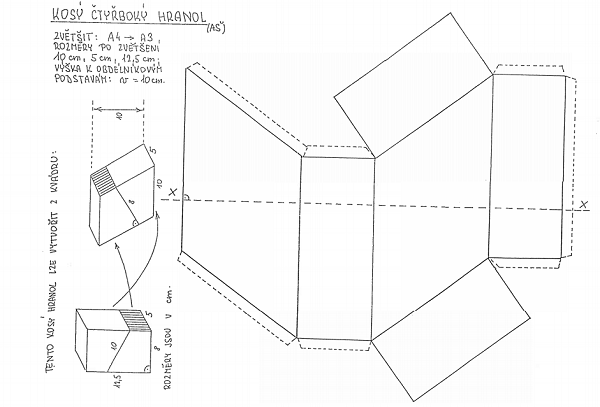
Na matrici je nakreslena síť našeho kosého hranolu ve zmenšeném měřítku. Pokud matrici zvětšíte (A4 -> A3), získáte síť, jejíž rozměry odpovídají popsanému modelu. Doporučuji síť oxeroxovat na polokarton. Model tak nabude potřebné pevnosti.
Ze sítě je patrný postup její konstrukce. Po složení modelu přejde úsečka XX do obvodu čtverce kolmého řezu hranolu. Odstřižením obdélníků podstav získáte plášť kosého hranolu. Můžete se přesvědčit, že tento plášť může být pláštěm celé řady dalších hranolů, jejichž podstavy budou kosodélníky se stranami dlouhými 5 cm a 10 cm.
Modely dvou shodných seříznutých kvádrů
Síť kosého hranolu můžeme též rozstřihnout podél úsečky XX, obě části doplnit obdélníkovými podstavami s rozměry 8 cm a 5 cm a příslušné mnohostěny slepit.
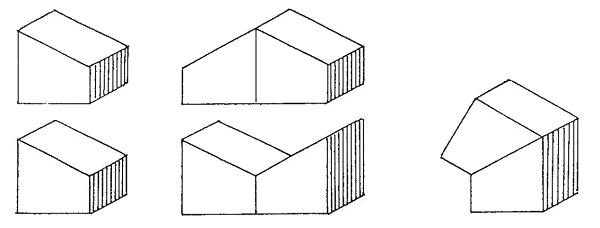
Z těchto částí podle potřeby složíme buď model kvádru nebo kosého hranolu, případně je můžeme užívat jako modely kolmých hranolů s lichoběžníkovými podstavami. Obě části je možné přikládat k sobě i jinými stěnami. Získáte tak třeba nekonvexní rovinově souměrné těleso atd.
Ideální sadou je ovšem tato sestava: Plný kvádr (nejlépe ze dřeva, aby byl dostatečně pevný), plný kosý hranol (též ze dřeva), pláště obou těchto mnohostěnů i jejich sítě a oba mnohostěny získané rozříznutím kvádru. Na této skupině pomůcek je možné demonstrovat téměř vše, o čem je ve škole v souvislosti s hranoly řeč. Tak – hodně zdaru!